La simulation consiste à créer un modèle informatique d’un système pour mieux comprendre et anticiper son comportement. La simulation de flux s’intéresse surtout à la capacité de production, aux files d’attentes et aux goulets d’étranglement.
Pourquoi simuler ?
L’exemple du garagiste.
Un garagiste reçoit dans son garage des véhicules à réviser. Ses journées font 10 h et il répare 12 voitures par jour (moyenne effectuée sur le trois derniers mois). Il sait qu’il passe en moyenne 40 minutes sur un véhicule pour un bénéfice de 50 €.
IL peut actuellement stationner des voitures en attente dans la rue.
Question : Quelle serait la taille idéale du parking dont il aurait besoin ?
L’approche mathématique. Importance et limitations.
Le but n’est pas de vous perdre. Vous pouvez passer rapidement sur les formules et aller au résultat.
Nous avons une file d’attente classique M/M/1 : les travaux à effectuer arrivent aléatoirement selon une loi exponentielle. Ils sont mis dans une file et sont traités dans l’ordre avec une durée qui suit aussi une loi exponentielle.
Les paramètres sont :
| Le nombre d’arrivées par heure. | taux d’arrivée | = 12/10 = 1.2 véhicules/heure |
| Le nombre de véhicules traités par heure. | taux de service | = 60/40 = 1.5 véhicules/heure |
L’intensité du trafic est ![]()
Notons que ![]() pour que la file soit stable et ne s’allonge pas à l’infini.
pour que la file soit stable et ne s’allonge pas à l’infini.
Les formules :
| Le nombre moyen de véhicules dans le système (attente + service) : | = 4.0 heures | |
| Le nombre moyen de véhicules en train d’être servis : | = 0.8 heures | |
| Le nombre moyen de véhicules en attente dans la file : | = 3.2 heures |
On trouve une moyenne de 3.2 véhicules en attente.
On peut aussi calculer le temps d’attente moyen dans la file : ![]() = 2.67 heures = 2 heures 40 minutes.
= 2.67 heures = 2 heures 40 minutes.
Résultat : le garagiste doit prévoir en moyenne 3.2 véhicules dans son parking.
Nous pouvons pousser les calculs pour voir dans quelle mesure 4 ou 5 places seront suffisantes. Cependant Les formules sont vites fastidieuse à une époque où nous avons de plus en plus besoin de réponses rapides.
Cependant il est primordial d’avoir au moins des notions pour ne pas se tromper.
Pour être efficace et ne pas commettre d’erreur, je pourrais rechercher sur Google un exemple de fichier Excel qui calcule les files d’attente. C’est déjà un modèle de simulation.
Attention, Chat GPT n’est pas un outil de simulation !
Par curiosité, voici la réponse de Chat GPT au problème posé :
La réponse de Chat GPT est plausible même si elle est fausse.
C’est bien là le danger. Chat GPT est un fantastique outil génératif mais le meilleur des outils ne nous dispense pas de savoir ce qu’on fait pour éviter les erreurs. C’est aussi vrai en simulation d’incendie où quelques notions de physique sont indispensables.
C’est également vrai en simulation de flux. Je pense néanmoins que l’utilisation d’un logiciel de simulation nous fait nous poser plus de questions : les clients déposent leur véhicule plutôt en début de matinée pour le récupérer le soir. Le garagiste est ouvert de 8h à 18h, mais le garagiste fait une pause de deux heures à midi, etc. C’est dans ce sens que la simulation aide à comprendre des systèmes parfois complexes.
Modèle de simulation de flux
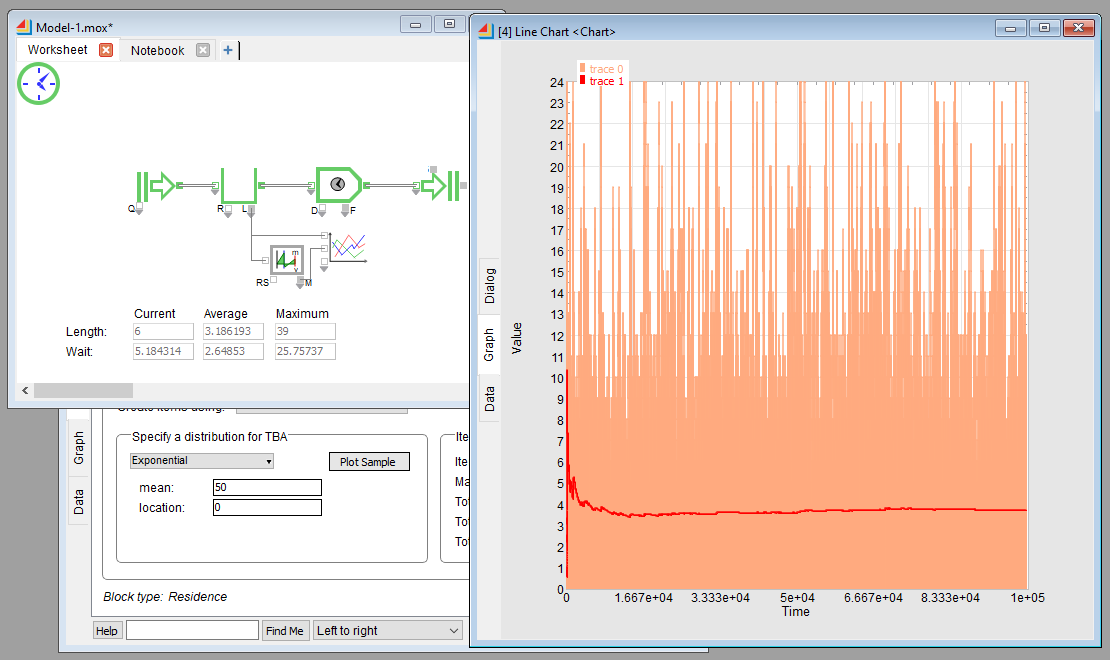
Le modèle informatique représenté ci-dessous utilise le logiciel ExtendSim et se crée en cinq minutes :
- Un bloc « Générateur » génère des entités avec un intervalle de temps de 50 minutes (loi exponentielle)
- Les entités entrent dans une file d’attente de capacité infinie par défaut.
- Un bloc « Activité » traite une entité en 40 minutes (loi exponentielle) avant de la libérer et de passer à l’entité suivante.
Le modèle simule en quelques secondes le fonctionnement du garage pendant 100000 heures d’ouvertures soit 10000 journées. Le graphique trace la longueur moyenne de la file de véhicule en attente. On voit que la courbe se stabilise bien autour de la moyenne théorique calculée : 3.2 véhicules.
Ce modèle pourrait répondre très facilement aux autres questions de l’exercice du garagiste consultable ici. Par exemple : la perte de bénéfice si le garagiste doit refuser des clients lorsque ses 4 places de parking sont occupées. Le garagiste se demande aussi s’il doit investir dans un second pont pour traiter les véhicules. L’exercice est volontairement simple mais se rapproche bien des vraies questions qui se posent en simulation de flux.
Merci au projet EnsROrice pour la présentation de l’exercice.